▶ 로지스틱 회귀 정의 & 비용함수 & 학습
1) 정의
→ 샘플이 특정 클래스에 속할 확률을 추정하는 것
→ binary(0 or 1)한 문제일 경우 주로 사용
2) 확률을 추정하는 법
→ 입력 변수의 가중치 합을 계산
3) 로지스틱 함수

p는 f(x) 값의 산출물
→ p < 0.5 이면 y = 0
→ p >= 0.5 이면 y = 1
4) 로지스틱 회귀 모델의 훈련
→ y = 1인 샘플은 높은 확률로, y = 0인 샘플은 낮은 확률로 추정하게 하는 최적의 가중치를 찾는 것이 목적
5) 로지스틱 회귀의 비용 함수
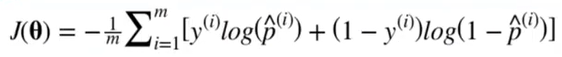
→ 비용함수는 p가 0에 가까워질수록 -log 값이 매우 커지고 1에 가까워질수록 0에 가까워진다.
→ positive한 샘플은 최대한 p를 1에 가깝게 만들어야 하고, negative한 샘플은 최대한 p를 0에 가깝게 만들어야 한다.
→ 비용함수는 2차함수(볼록함수)이므로 경사하강법 혹은 다른 최적화 알고리즘을 통해 전역 최소값을 찾을 수 있다.
6) 실습
- 붓꽃 데이터 사용
→ 세 개의 품종 (Setosa, Versicolor, Virginica), 150개의 데이터 수, Petal(꽃잎) Sepal(꽃받침)의 너비와 길이를 가짐

위와 같이 iris 데이터 로드

x : 콜론을 하나 더 찍어서 2차원 배열로 만들어주기
y : versicolor가 뜨면 1, 아니면 0을 출력

위와 같이 defualt 값으로 모델의 데이터 학습

linspace() : 0~3 사이의 1000개 데이터 임의로 생성해주는 함수

위에서 학습시켰던 모델을 예측해본 것

x_new.shape은 (1000,1)인데 y_proba.shape은 (1000,2)가 나옴
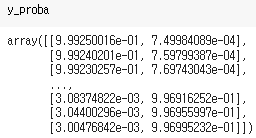
결과를 보면 [Versicolor가 아닐 확률, Versicolor일 확률]을 출력
→ 앞쪽데이터는 Versicolor가 아닐 것이라고 예측, 뒤로 갈수록 Versicolor일 것이라고 예측
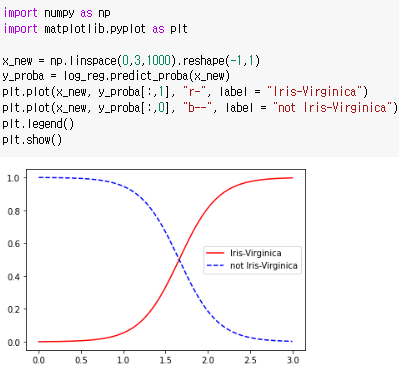
시각화한 결과 Virginica는 너비가 약 1.4~2.5에 분포하고 있음을 알 수 있다.
▶ 소프트맥스 회귀
1) 정의
→ categorical(여러 클래스 분류)한 문제일 경우 주로 사용
2) 소프트맥스 함수
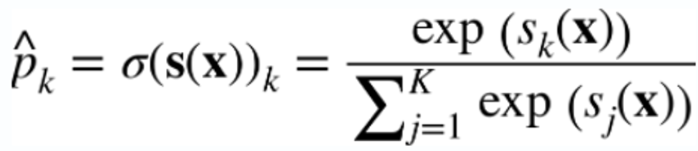
3) 소프트맥스 회귀 분류기의 예측
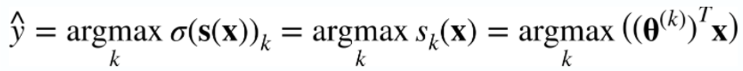
→ 여러 클래스 중에서 확률 값이 가장 높은 것을 실제 클래스라고 예측
4) 크로스 엔트로피
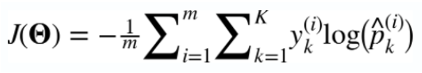
→ 추정된 클래스의 확률이 목표 클래스에 얼마나 잘 맞는지 판단하는 용도로 사용
5) 실습


multinomial을 표시하여 소프트맥스 회귀 사용 가능
solver: ibfgs -> 기본적으로 머신러닝 분야에서 많이 사용
C : L2 규제화 -> weight 값에 square 값을 해준 것

가장 큰 인덱스 값을 출력했을 때 위와 같이 virginica가 나오는 것을 확인할 수 있다.

위와 같이 predict_proba를 이용하여 값을 확인하는 것도 가능하다.
▶ 서포트 벡터 머신
1) 정의
→ 매우 강력하고 선형, 비선형 분류, 회귀 이상치 탐색에 사용할 수 있는 다목적 머신러닝 모델
→ 복잡한 분류 문제에 잘 들어맞고, 작거나 중간 크기의 데이터셋에 적합
→ 특성 스케일에 아주 민감
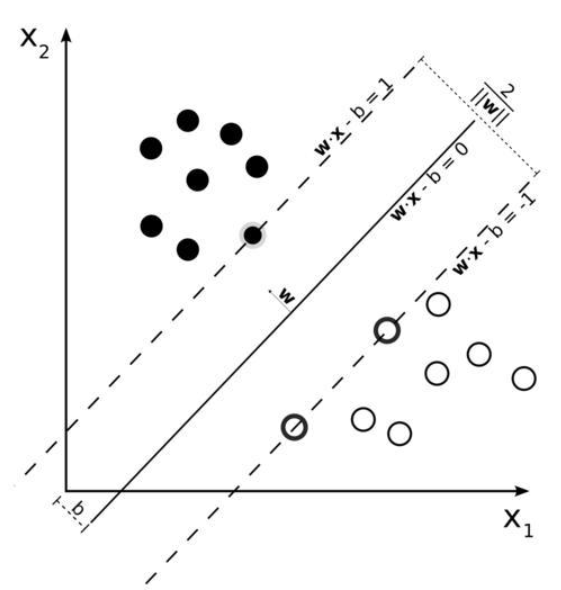
2) 서포트 벡터 머신의 분류
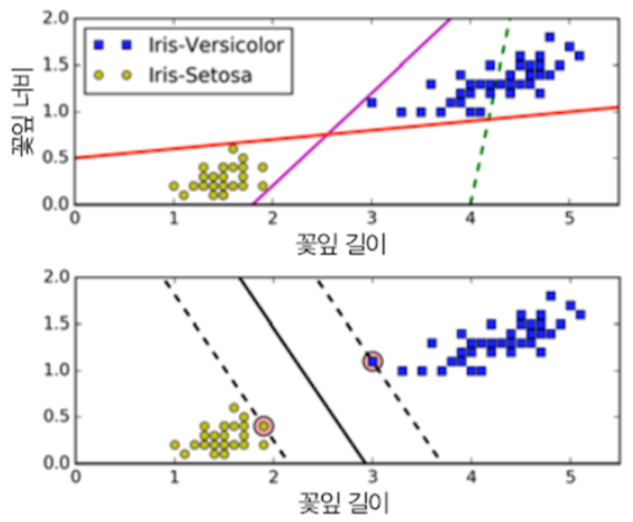
→ 첫번째 그림의 두 분류기는 정확히 분류는 하고 있으나 모델 분류기의 선이 훈련 데이터와 너무 가까워서 새로운 데이터가 들어왔을 때 정확히 분류하지 못할 수 있다.
→ SVM의 목적은 classfier를 할 때 클래스를 나누는 결정경계가 훈련샘플로부터 최대한 멀리 떨어뜨려 놓는 것이다.
→ 즉, SVM 분류기는 클래스 사이의 가장 폭이 넓은 구간을 찾는 것으로 이해할 수 있다
→ SVM은 특성 스케일에 민감하므로, 보통 사이킷런의 StandardScaler을 사용하면 결정경계의 명확성을 높일 수 있다.
3) 실습
① 선형 SVM 분류
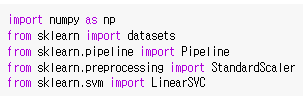
pipeline은 데이터 스케일과 모델 적합을 한 번에 할 수 있다.
LinearSVC를 통해 SVM을 사용할 수 있다.


C는 규제항, loss는 hingeloss를 의미한다.

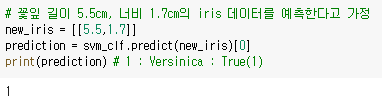
위와 같이 예측값이 1로 잘 나오는 것을 확인할 수 있다.
② 비선형 SVM 분류
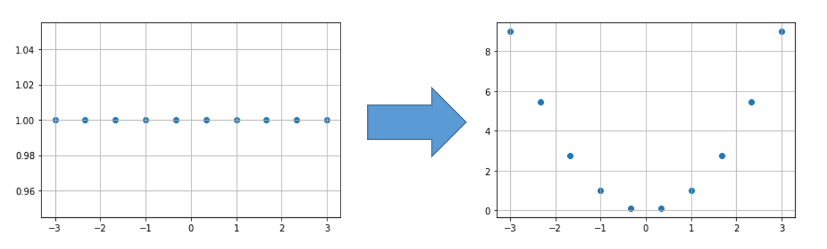
위와 같은 경우에 비선형 SVM을 사용할 수 있다.
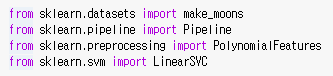



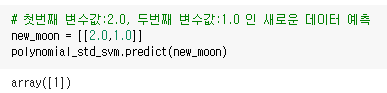
비선형 SVM은 Polynomial라는 변수 변환을 통해 할 수 있다.
※ SVM Hinge Loss
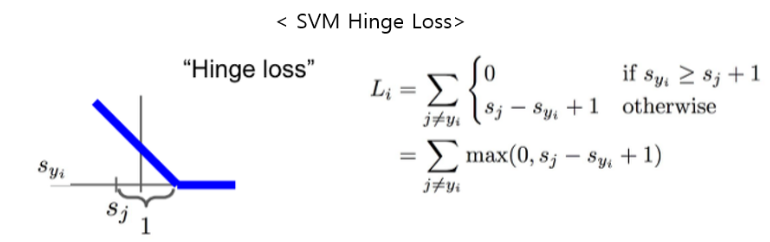
SVM에서 사용하는 기본적인 hinge loss 값은 위와 같다.
▶ 커널 서포트 벡터 머신
▷ 다항식 커널
→ 다항식 특성을 추가하는 것처럼 간단하고 모든 머신러닝 알고리즘에서 잘 동작한다.
→ SVM 사용 시 kernel trick이라는 수학적 기교를 사용하여 실제로 특성을 추가하지 않았음에도 불구하고 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다.

▷ 가우시안 RBF 커널
→ 다항 특성 방식과 마찬가지로 유사도 특성 방식을 모델에 적용할 수 있다.

'WINS STUDY > 파이썬 기초 라이브러리부터 쌓아가는 머신러닝' 카테고리의 다른 글
| 섹션 2. 선형 회귀 이론 및 실습 (0) | 2022.08.13 |
|---|---|
| 섹션 1. Matplotlib & Seabor 라이브러리를 활용한 데이터 시각화 (0) | 2022.08.06 |
| 섹션 0. Pandas 라이브러리를 활용한 데이터 전처리 (0) | 2022.07.29 |